Ch. 07, Sec. A

$\newcommand{\ddfrac}[2]{\frac{\displaystyle{#1}}{\displaystyle{#2}}}$

Exercises

Ex. 11

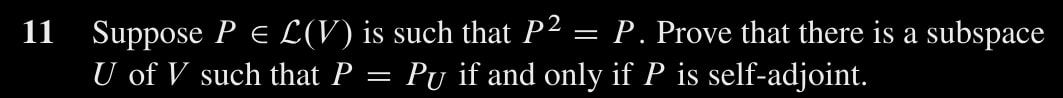
$(\rightarrow)$ Observe $v = v_U + v_{U^\bot}$ and $w = w_U + w_{U^\bot}$. Clearly, \begin{aligned} \langle Pv, w \rangle &= \langle v_U, w \rangle \\ &= \langle v_U, w_{U^\bot} \rangle + \langle v_U, w_U \rangle \\ &= 0 + \langle v_U, w_U \rangle \\ \langle v, Pw \rangle &= \langle v_{U^\bot}, w_U \rangle + \langle v_U, w_U \rangle \\ &= 0 + \langle v_U, w_U \rangle \end{aligned}

$(\leftarrow)$ For $U = range \ T$ and $v = v_U + v_{U^\bot}$, we show $Tv = v_U$.

Lemma. $Tv_U = v_U$.

Since $v_U \in range \ T$, by definition we know $Tv_0 = v_U$. So $T(Tv_0) = Tv_0$ as $T^2 = T$, which concludes $Tv_U = v_U$.

Lemma. $Tv_{U^\bot} = 0$.

By definition we know $v_{U^\bot} \in (range \ T)^\bot$. But given $T$ is self-adjoint, $(range \ T)^\bot = null \ T$. So $v_{U^\bot} \in null \ T$.

In conclusion, $Tv = Tv_U + Tv_{U^\bot} = v_U + 0 = v_U$.

Ex. 17

Fact. For $normal \ T$, $range \ T$ = $range \ T^*$ and $null \ T = null \ T^*$. For any $T$, $range \ T = (null \ T^*)^\bot$. See ex.16.

Lemma. For $normal \ T$, $range \ T \cap null \ T = {0}$.

Observe $L.H.S = (null \ T^*)^\bot \cap (null \ T^*)$ by the aforementioned facts.

Theorem. $null \ T^k = null \ T$.

Clearly $null \ T \subset null \ T^k$ as $T0 = 0$ for any operator $T$. It remains to show $null \ T^k \subset null \ T$.

$v \rightarrow^T v_1 \rightarrow^T v_2 \rightarrow^T \dots \rightarrow^T v_k = 0$.

$v_{k-1} \in range \ T \cap null \ T$, so $v_{k-1} = 0$.

…

$v_1 \in range \ T \cap null \ T$, so $v_1 = 0$.

Thus $Tv = v_1 = 0$, and $v \in null \ T$.

Theorem. $range \ T^k = range \ T$.

Let $T’$ be the same as $T$ but restricted on subspace $range \ T$. Observe it is a linear operator.

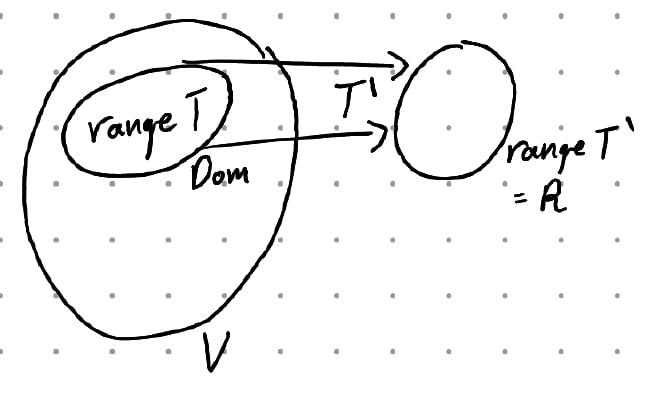
We prove $null \ T’ = {0}$. Observe for $v \in null \ T’$, $v \in range \ T \cap null \ T$, and hence $v = 0$. Clearly $T'0 = 0$ as $T0 = 0$ for any operator $T$.

It follows $dim \ null \ T’ = 0$. By The Fundamental Theorem of Linear Maps (See Axler page 63), $dim \ range \ T = dim \ range \ T’$. But by definition $range \ T’ \subset range \ T$, and therefore $range \ T’ = range \ T$.

We conclude $T[range \ T] = range \ T$, The image of $range \ T$ under $T$ is exactly $range \ T$. Clearly it suffices to prove our intended theorem.

Ex. 19

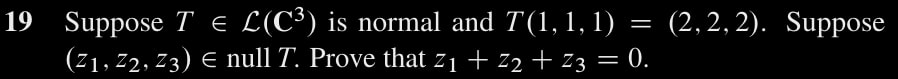
By normality we know $null \ T = (range \ T)^\bot$. So $(z_1, z_2, z_3) \bot v$, for any $v \in ran \ T$. It follows \begin{align*} (z_1, z_2, z_3) \cdot v &= 0 \\ (z_1, z_2, z_3) \cdot T(1, 1, 1) &= 0 \\ &= (z_1, z_2, z_3) \cdot (2, 2, 2) = 2 z_1 + 2 z_2 + 2 z_3 = 2 (z_1 + z_2 + z_3) \end{align*} Thus $z_1 + z_2 + z_3 = 0$.