Guarini's Puzzle, A Less Elegant Solution

Hold on your keyboard as a google search on Guarini’s puzzle shall show you not only the problem but also its solution as well. In fact, The solution yielded by google is far more elegant than mine presented here. So, Don’t do it if you wish to appreciate this blog post. Nonethless, I am really proud that I solved the problem on my own. The sole prerequisite to reading this post is how to move a knight in a chess board.

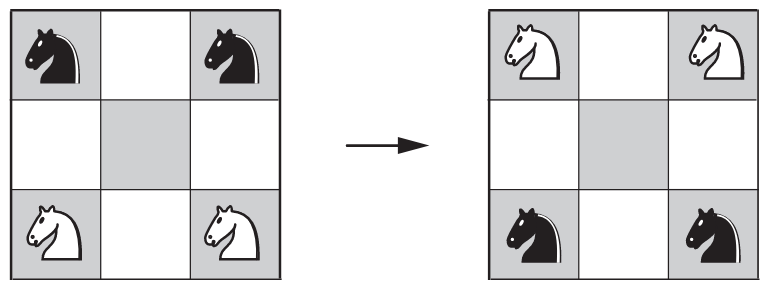
Puzzle

The puzzle basically asks you to interchange the two black knights with the two white knights in a 3x3 board as shown above.

For the sake of my own convenience, I am going to illustrate it as 3x3 table where x denotes black knights and o denoted white knights as follows.

From

x	.	x
.	.	.
o	.	o

To

o	.	o
.	.	.
x	.	x

Simpler Version

Let’s consider a simpler problem than the one we are currently solving, Then see whether we could generalize it back to the original one. We have one black knight and wish to move it to the bottom-left cell.

From

.	.	x
.	.	.
.	.	.

To

.	.	.
.	.	.
x	.	.

Remark: Interchangeable Positions

Wherever our knight’s position is or where it is heading, There are two areas of the board it is interchangeably moving between. Namely,

plus shape

.	#	.
#	.	#
.	#	.

x shape

#	.	#
.	.	.
#	.	#

Note that the center cell is unreachable at all.

Remark: Unique Path

Let’s begin doing some trials. We begin from the initial position stated above. We have two alternative moves

move 1

.	.	x
x	.	.
.	.	.

move 2

.	.	x
.	.	.
.	x	.

Let’s put move 2 aside now and proceed with move 1. Then we have

move 1-1

.	.	x
x	.	.
.	.	.

move 1-2

.	.	.
x	.	.
.	.	x

move 1-1 returns us back to a state we already visited. All paths which stem from it are already considered and hence, redundant to us. So, we need to consider only move 1-2.

move 1-2-1

.	.	.
x	.	.
.	.	x

move 1-2-2

.	x	.
.	.	.
.	.	x

Again, move 1-2-1 returns us to state we already visited. So, We drop it from our considerations. A similar justification shows the next move is

move 1-2-2-2

.	x	.
.	.	.
x	.	.

which reaches us to our desired goal. This discussion clearly shows there is a unique path from move 1 to the goal.

What about move 2? Does it yield a different path than the one we just found? The answer is yes. Nonethless, We are going to drop it as well!

Remark: Symmetry

Here is the state we are in doubt of finding a new path from

move 2

.	.	x
.	.	.
.	x	.

We rotate the board 90 degrees to the right, Then flip it on its x-axis.

rotation

.	.	.
x	.	.
.	.	x

flip

.	.	x
x	.	.
.	.	.

Which is exactly move 1 we considered before! In fact, the whole path which stems from move 2 is exactly the same as move 1 but seen from a different perspective. At this point you might wish to do some trials on your own to see the two equivalent paths from two different perspectives.

Concluding For a General Approach

We focus our attention on the one unique path we found regardless of its different representations/perspectives due to board’s symmetry. Could we move all knights on this path? Could board’s symmetry allow us to re-interpret each knight’s path as the unique path we discussed earlier?

For the top-left black knight. If we rotated the board 90 degrees to the right, We could re-interpret it as a top-right black knight which wishes to reach bottom-left cell.

For the bottom-left white knight. If we rotated the board 180 degrees to the right, We could re-interpret it as a top-right black knight which wishes to reach bottom-left cell.

For the bottom-right white knight. If we rotated the board 270 degrees to the right, Similarly, We could re-interpret it as following the unique path we found.

Note that for an interation, If we moved each knight one step as we just illustrated, We see the two areas we highlighted in remark: interchangeable positions are fully covered interchangeably.

Solution

As we just noted, Let’s just move each knight one step in the unique path we found for an iteration.

x	.	x
.	.	.
o	.	o

Iteration: 1

x	.	x
x	.	.
o	.	o

x	.	.
x	.	.
o	x	o

.	.	.
x	.	o
o	x	o

.	o	.
x	.	o
.	x	o

.	o	.
x	.	o
.	x	.

Iteration: 2

.	o	.
x	.	o
.	x	x

.	o	x
.	.	o
.	x	x

o	o	x
.	.	o
.	.	x

o	o	x
.	.	.
o	.	x

o	.	x
.	.	.
o	.	x

Iteration: 3

o	x	x
.	.	.
o	.	x

o	x	x
x	.	.
o	.	.

o	x	.
x	.	.
o	o	.

.	x	.
x	.	o
o	o	.

.	x	.
x	.	o
.	o	.

Iteration: 4

.	x	.
x	.	o
x	o	.

.	.	.
x	.	o
x	o	x

.	.	o
.	.	o
x	o	x

o	.	o
.	.	o
x	.	x

o	.	o
.	.	.
x	.	x

tdaa !!

Conclusion

Now I think it is time to google Guarini’s puzzle to see a more elegant solution than the one presented here. By the way, I am not jealous if you liked it more than mine.